序

在阅读本文前，请务必对 Trie （字典树）有一定的了解。

$\text{AC}$ 自动机 ( $\mathtt{Aho-Corasick-Auto-Manton}$ ) ，相必各位刚来到洛谷时点开算法标签，就对在第一个板块中尤为显眼的它产生了兴趣。

而他的功能并不像名字那般玄幻， 只是用于实现字符串多对单匹配罢了。

何为多对单匹配?

给定一个字符串集合 $P$, 还有一个文本串 $T$, 试问有多少个 $P$ 中的串在 $T$ 中出现过？

你就会说了：“跑 $|P|$ 次 KMP” 不就好了？

真实的你：“KMP是啥，好吃吗？”

不过，当你用 $P_i$ 跑 KMP 时，若有 $P_j$ 是 $P_i$ 的子串，则跑 $P_j$ 时就浪费了很多时间。

我们可以借鉴 Tarjan 求 LCA 的思想，既然对被询问的东西做不了手脚，那就对询问的东西做手脚。

“把 $P$ 建成一颗 Trie ！”

$\text{Aho Corasick}$ 在 1975 年想到了。

初始化

例子：

若文本串 $T=\mathtt{hesherit}$。

字符串集 $P=\{\mathtt{he},\mathtt{she},\mathtt{it},\mathtt{her},\mathtt{qwq}\}$。

则初始的 $\mathtt{trie}$ 如下图：

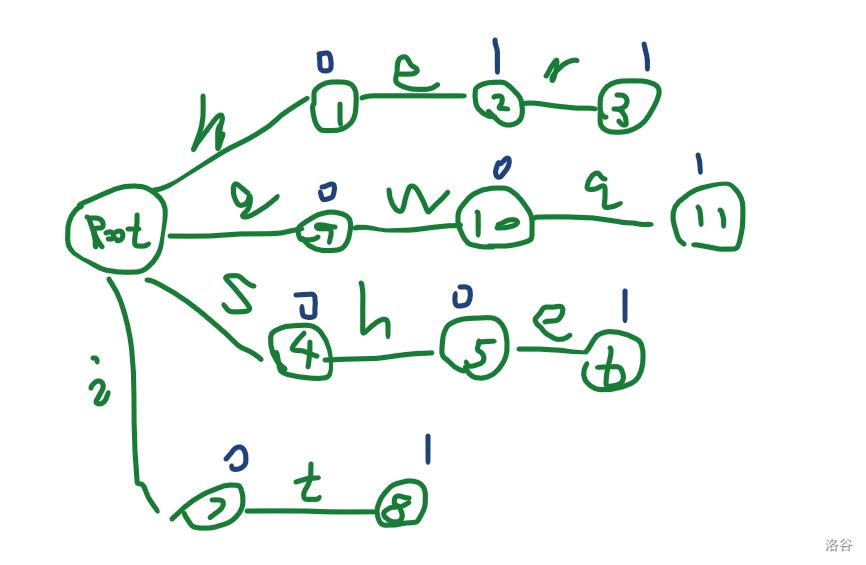
其中，蓝笔标的是 $\mathtt{cnt}$ 数组的值，$\mathtt{cnt}(i)$ 表示从根节点到 $i$ 的这条路径形成的字符串（下文记作 $pt_i$）在 $P$ 中是否出现。

朴素匹配的劣处与失配指针的引入

在某一位失配以后，朴素的想法是从开始匹配的位置下一位重新开始，但我们显然可以用一些思想来优化这个过程。

比如，我们匹配 $\mathtt{her}$ 时在 $\mathtt{hes}$ 失配了，从 $esh$ 开始显然是浪费时间的。

那怎么办呢？

匹配既然要移动，那么当前匹配的字符串的一个前缀必定是失配子串的一个后缀，我们直接移动到最长公共前后缀处开始匹配即可。

由于 $\mathtt{trie}$ 的性质，我们可以用 $\mathtt{fail}$ 指针来记录这个过程。

失配指针的形式化定义

形式化地，$\mathbf{f}_i$ 记录 $pt_i$ 在 $\mathtt{trie}$ 中的最长后缀的位置。

例如 $\mathbf{f}_6=2$，由于 $\mathtt{she}$ 出现过的最长后缀是 $\mathtt{he}$，而 $pt_2=\mathtt{he}$。

失配指针的构建

隆重地介绍两个由 lls 提出的法则：平行四边形法则与三角形法则。

平四法则

如果节点 $u$ 沿着字符 $c$ 来到了存在于 $trie$ 中一个点 $v$，则 $\mathbf{f}_v$ 为 $\mathbf{f}_u$ 沿着 $c$ 走到的节点编号。

感性理解：由于 $pt_{\mathbf{f}_u}$ 是 $pt_u$ 的后缀，显然 $pt_u+c=pt_{\mathbf{f}_u} + c$，又因为 $pt_{\mathbf{f}_u}$ 是最长后缀，所以 $pt_{\mathbf{f}_v}$ 也是最长的。

画出来大概就是这个样子：

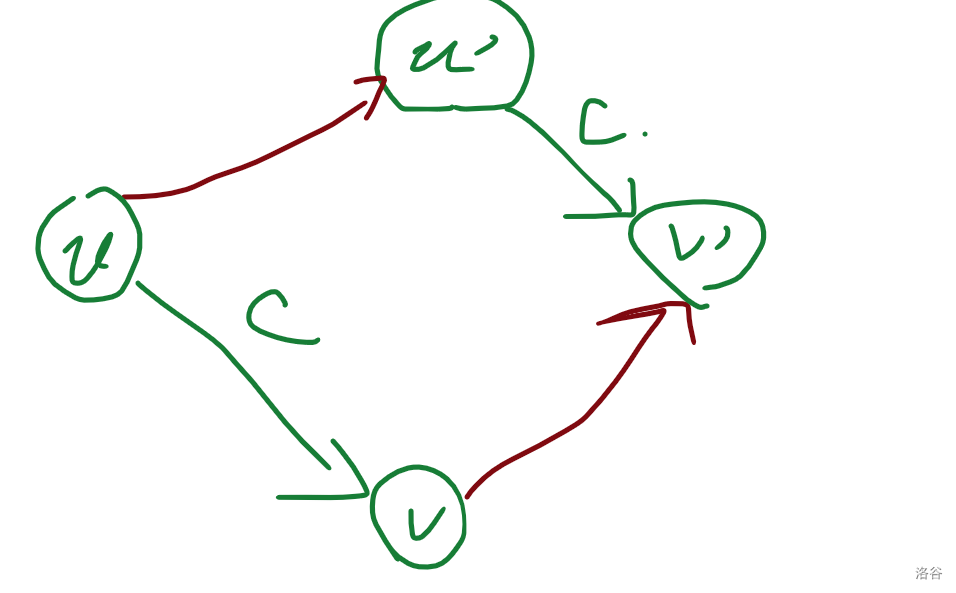
（红色的是失配指针，绿色的是原来的边和点）

三角法则

若 $u$ 沿着 $c$ 来到了一个不存在的点 $v$，那么如果匹配时也走了这条边，那么就失败了，所以 $v$ 是一个失配点，直接把这条边连向失配指针就好了，这样查询的时候就可以无脑沿着失配指针跳了。

画出来大概就是这个样子：

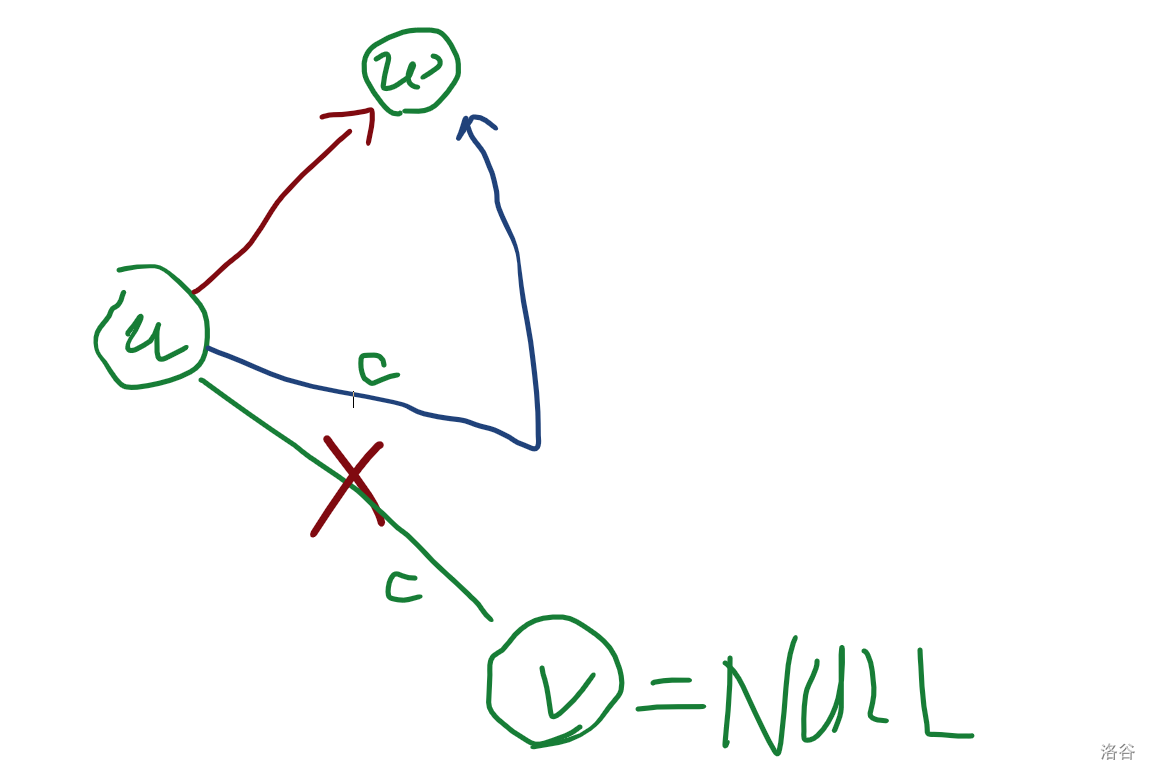
（红色的是失配指针，绿色的是原来的边和点，蓝色的是新的边）

代码实现

容易发现，当前节点的构建依赖于它的前驱节点，所以用 $\mathtt{BFS}$ 实现。

void build() {

// nt 为 fail 指针

vector<int> que;

for (int i=0; i<LMT; ++i) if (c[0][i]) {

nt[c[0][i]] = 0, que.push_back(c[0][i]);

} // 先将与根相连的节点进队

for (int b = 0; b < que.size(); b++) {

for (int i = 0; i < LMT; i++) { // LMT 为可用字符数量，通常为26

int v = c[que[b]][i];

if (v) nt[v] = c[nt[que[b]]][i], que.push_back(v); //平四

else c[que[b]][i] = c[nt[que[b]]][i]; //三角

}

}

}

查询

我们在自动机里不断跳来跳去，并且加上贡献，注意去重。

int get(string s) {

int u=0, r=0; // u:当前节点 r:答案

for (char d:s) {

int i = app(d); // app 为转换函数，将字符转换为编号

u = c[u][i]; // 沿着这条边走过来

for (int j = u; j && ~mark[j]; j = nt[j]) // 不断在失配节点里跳

r += cnt[j], mark[j]=-1; // mark 用来打标记去重

}

return r;

}

后记

感觉也不是那么难嘛，lls 牛逼！

贴一个我的板子吧：

//N: 自动机大小

//TAG == 0: 仅包含大写字母

//TAG == 1: 仅包含小写字母

//TAG == 2: 大小写均有

template<const int N, const int TAG>

struct Aho_Corasick {

int LMT, tot, nt[N], cnt[N], c[N][60], mark[N];

int app(char ch) {

if (!TAG) return ch-'A';

if (TAG==1) return ch-'a';

if(ch <= 'Z') return ch-'A';

return 26+ch-'a';

}

void insert(string s) {

int u=0;

for (char d:s) {

int i=app(d);

if(!c[u][i]) c[u][i] = ++tot;

u = c[u][i];

}

cnt[u]++;

}

void insert(char *s) {

int u=0;

int n=strlen(s);

for (int j=0; j<n; ++j) {

int i=app(s[j]);

if(!c[u][i]) c[u][i] = ++tot;

u = c[u][i];

}

cnt[u]++;

}

void build() {

vector<int> que;

for (int i=0; i<LMT; ++i) if (c[0][i]) nt[c[0][i]] = 0, que.push_back(c[0][i]);

for (int b = 0; b < que.size(); b++) {

for (int i = 0; i < LMT; i++) {

int v = c[que[b]][i];

if (v) nt[v] = c[nt[que[b]]][i], que.push_back(v);

else c[que[b]][i] = c[nt[que[b]]][i];

}

}

}

int get(string s) {

int u=0, r=0;

for (char d:s) {

int i = app(d);

u = c[u][i];

for (int j = u; j && ~mark[j]; j = nt[j])

r += cnt[j], mark[j]=-1;

}

return r;

}

int get(char* s) {

int u=0, r=0, nnn = strlen(s);

for (int jjj=0; jjj<nnn; ++jjj) {

int i = app(s[jjj]);

u = c[u][i];

for (int j = u; j && ~mark[j]; j = nt[j])

r += cnt[j], mark[j]=-1;

}

return r;

}

int qry(char *s) {

memset(mark, 0, sizeof(mark));

return get(s);

}

int qry(string s) {

memset(mark, 0, sizeof(mark));

return get(s);

}

Aho_Corasick() {

LMT=(TAG==2 ? 52 : 26);

memset(cnt, 0, sizeof(cnt));

memset(c, 0, sizeof(c));

tot=0;

}

Aho_Corasick(vector<string> SS) {

LMT=(TAG==2 ? 52 : 26);

memset(cnt, 0, sizeof(cnt));

memset(c, 0, sizeof(c));

tot=0;

for (string s:SS) insert(s);

build();

}

Aho_Corasick(string* SS, int _n) {

LMT=(TAG==2 ? 52 : 26);

memset(cnt, 0, sizeof(cnt));

memset(c, 0, sizeof(c));

tot=0;

for (int i=1; i<=_n; ++i) insert(SS[i]);

build();

}

Aho_Corasick(char** SS, int _n) {

LMT=(TAG==2 ? 52 : 26);

memset(cnt, 0, sizeof(cnt));

memset(c, 0, sizeof(c));

tot=0;

for (int i=1; i<=_n; ++i) insert(SS[i]);

build();

}

};